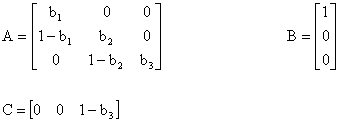|
Si
indichino con x1(t), x2(t) e x3(t) il
numero di allievi in prima, seconda e terza durante il t-esimo anno scolastico
(cioè nel periodo 15 settembre - 15 giugno) e con u(t) il numero
di allievi che si iscrive in prima alla fine dell’anno t e che quindi frequenterà
nell’anno scolastico (t+1). Conoscendo la porzione di bocciati nell’i-esima
classe si può allora scrivere
e
il numero y(t) di diplomati ogni anno sarà dato da
Iscritti
(u(t)) e diplomati (y(t)) sono pertanto ingresso ed uscita di un sistema
lineare del terzo ordine
Questo
sistema è completamente
osservabile perché la matrice di osservabilità
è
non singolare (purché
). Questo permette di affermare che noti, ad esempio, u(0), u(1),
y(0), y(1) e y(2) è possibile determinare x1(0), x2(0)
e x3(0) e quindi (dalle equazioni di stato) xi(t)
per ogni t>0. |
