soluzione tasse inquinamento

Si tratta di un problema di pianificazione assai particolare in quanto la decisione viene presa dallo stato o dall’ente incaricato della tutela delle acque ( d’ora in poi chiamato “agenzia di bacino”) una volta per tutte, fissando il tipo di tassa che ciascun utente deve pagare, ma non è noto a priori quali utenti decideranno di insediarsi nel sistema né dove. In questo senso quindi le variabili di decisione sono più ridotte di quelle che si ipotizzano normalmente nei problemi di pianificazione (una agenzia di bacino autoritaria potrebbe decidere a priori quali utenti possano sfruttare il fiume e in quali posizioni).

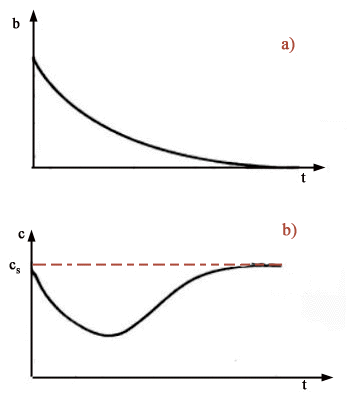
Sotto un altro punto di vista il problema potrebbe essere classificato come “a molti decisori” in quanto ciascun utente è completamente libero di fare le proprie scelte, pur di sottostare ovviamente ai vincoli legislativi in vigore.

Prima di passare ad analizzare il problema più in dettaglio, ricordiamo che le sostanze biodegradabili immesse in un corso d’acqua vengono demolite dai batteri i quali, per compiere questa operazione, consumano una certa quantità di ossigeno. Si può assumere (si veda il modello di Streeter e Phelps o una sua estensione presentata in un altro esercizio) che il decadimento dell’inquinante presente avvenga in modo proporzionale alla concentrazione dell’inquinante stesso e che ciò provochi un analogo consumo di ossigeno. Quest’ultimo viene reintegrato attraverso lo scambio con l’atmosfera in modo proporzionale alla differenza tra la concentrazione di saturazione c_s (alla temperatura cui si trova il fiume) e l’ossigeno c attualmente presente. Sotto queste ipotesi l’andamento della concentrazione di inquinante (b) e di ossigeno (c) a valle di un punto di scarico, hanno il tipico andamento riportato nelle Fig. 2a e 2b.

Naturalmente se un altro scarico entra nel fiume prima che l’inquinante sia completamente degradato i due effetti si sommeranno e si potrà pertanto avere un ulteriore abbassamento del valore minimo dell’ossigeno.

Prima di decidere se installarsi o meno nell’area un utente (supporremo d’ora in poi che si tratti di una industria) valuterà la differenza tra i profitti che può ottenere dalla propria attività e la tassa imposta dall’agenzia di bacino. Naturalmente sarà suo interesse far sì che sia massima la differenza tra profitti e costi. Ogni utente risolverà quindi un problema di massimo rispetto alle due variabili di cui egli detiene il controllo, vale a dire la quantità q di inquinante da scaricare (e quindi le dimensioni dell’attività produttiva) e la posizione l lungo il fiume alla quale insediarsi. E’ infatti evidente che le tasse che dovrà pagare per riversare una data quantità di inquinante saranno alquanto diverse a seconda che lo scarico vada ad aggravare una situazione già molto vicina al limite c^* oppure sia invece in una zona a valle della quale l’inquinamento è modesto.

in cui il profitto è proporzionale all’inquinante prodotto q secondo il coefficiente a_i. Tale coefficiente varierà ovviamente da settore a settore produttivo e anche all’interno dello stesso settore per la diversa efficienza dei singoli impianti.

Per risolvere il proprio problema l’utente dovrà richiedere l’andamento della funzione t(q, l) all’agenzia di bacino la quale potrà calcolarla in base ai dati di qualità del fiume noti fino a quel momento, tramite un opportuno modello matematico. Nota che sia questa funzione l’utente sceglierà una certa posizione l e il valore q dello scarico in modo da ottimizzare il proprio beneficio. Si noti che, se i valori di a_i sono bassi (produzioni scarsamente remunerative o molto inquinanti) è possibile che la differenza tra profitti e tasse sia, anche all’ottimo, negativa e quindi l’utente decida che non è conveniente installarsi nel bacino. Se invece il beneficio ottimo è positivo l’utente entrerà nel sistema e i suoi valori di posizione e scarico entreranno a far parte dei dati in base ai quali l’agenzia di bacino elaborerà la funzione t(q, l) da proporre all’utente successivo.

Date queste premesse è facile prevedere che le prime industrie si insedieranno verso la foce del fiume (o comunque verso la fine del tratto sottoposto al controllo dell’agenzia) in quanto così facendo potranno, a parità di scarico, pagare tasse minori. Man mano poi che si esaurirà lo spazio fisico e il fiume diverrà più inquinato lo sviluppo avanzerà verso monte e sempre più frequentemente le potenziali industrie dovranno abbandonare l’idea di installarsi nell’area. I loro coefficienti a_i saranno cioè troppo bassi per bilanciare le tasse richieste dall’agenzia di bacino. Verranno così selezionate automaticamente solo le industrie con redditività elevata rispetto all’inquinamento prodotto. Le industrie si disporranno inoltre in modo che il picco di deficit generato da ciascuna sia sfasato rispetto a quello creato dalle industrie già installate in modo da mantenere il più possibile la concentrazione di ossigeno lontana dallo standard prefissato.

E’ interessante notare che in ogni istante, fissate le industrie presenti, il sistema si trova nella situazione detta di equilibrio di Nash, nella quale nessun utente ha interesse a modificare per primo le proprie decisioni (in particolare la quantità q di inquinante scaricata, dato che modificare la posizione è, da un punto di vista pratico, assai più problematico). Ferma restando infatti la sua produttività, determinata dal coefficiente a_i, egli non aumenterà nè diminuirà il proprio scarico perché ciò implicherebbe una diminuzione del suo beneficio. Per gli stessi motivi il sistema si trova anche in condizioni di ottimo paretiano, perché nessuna azienda può aumentare i propri utili se non diminuendo quelli di un’altra. Ciò non toglie che esista la possibilità che più utenti si coalizzino per ottenere complessivamente benefici maggiori, incrementando la produzione delle imprese più efficienti e rifondendo, con il surplus di benefici ottenuti, quelle meno efficienti che siano costrette a ridurla.

Dopo un certo periodo di tempo, e quindi dopo l’entrata nel sistema di numerose industrie, la concentrazione di ossigeno disciolto nel fiume tenderà ad avvicinarsi ad una concentrazione di ossigeno costante lungo tutto il corso e prossima al valore c^*, ovviamente senza mai raggiungere tale limite dato che le tasse in questo caso diventerebbero infinite. L’insediamento di nuove aziende risulterà sempre più difficile a causa degli elevati valori di redditività richiesti per rendere conveniente l’avvio delle attività. Il sistema si troverà dunque in una situazione relativamente stabile, tuttavia a nessun utente sarà a priori preclusa la possibilità di accedere alla risorsa.

Infine, se una configurazione con concentrazione di ossigeno costante non fosse ritenuta soddisfacente (nel caso si volesse, ad esempio, garantire una concentrazione di ossigeno più elevata in un tratto di fiume destinato a scopi particolari) lo schema di tassazione potrebbe essere ancora adottato pur di modificare opportunamente il valore limite c^* rendendolo variante lungo il corso del fiume.