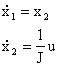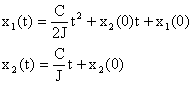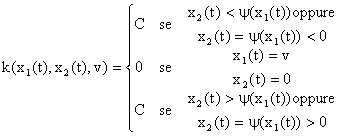|
Le
equazioni di stato del sistema sono
ed
il problema consiste nel determinare una legge di controllo
che
faccia sì che l’antenna inizialmente in
si
trasferisca nel più breve tempo possibile nello stato
e
vi rimanga finché il segnale v non venga variato (cioè finché
non si desideri puntare l’antenna in una nuova direzione). La legge di
controllo deve pertanto essere tale che
poiché
quando l’antenna è ferma (x2 =0) nella posizione desiderata
(x1 = v), il motore non deve esercitare alcuna coppia (u=0).
D’altra
parte è intuitivo che, per effettuare l’operazione in tempo minimo,
in tutte le altre condizioni
il motore deve funzionare a coppia massima. Naturalmente si dovrà
avere 
o 
a seconda dei valori di posizione (x1(t)) e velocità
(x2(t)) dell'antenna. In altre parole, la legge di controllo 
dovrà comunque essere una funzione non lineare che assuma soltanto
tre possibili valori (+C, 0, -C) che corrispondono rispettivamente alle
condizioni di massima accelerazione, fermo e massima decelerazione.Per
determinare la legge di controllo calcoliamo, innanzitutto, il movimento
dell’antenna con motore funzionante a coppia massima.
Le
equazioni di stato sono in questo caso
per
cui integrando si ottiene
Le
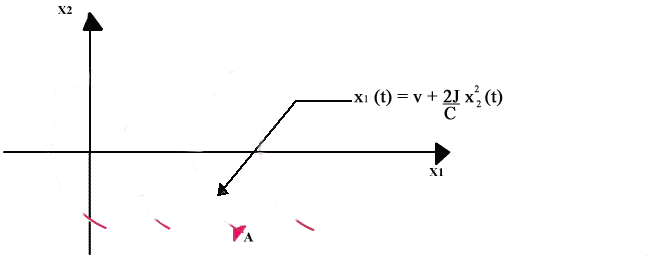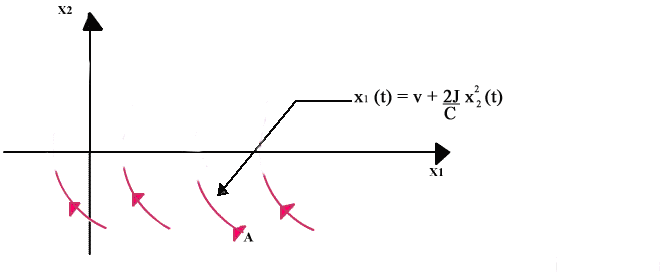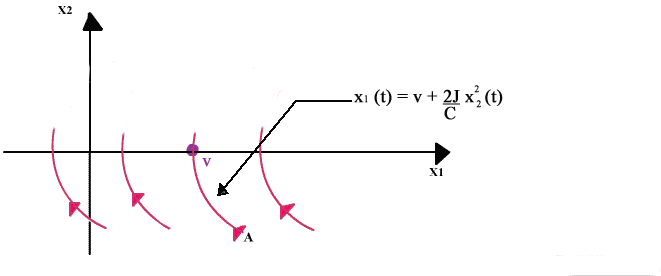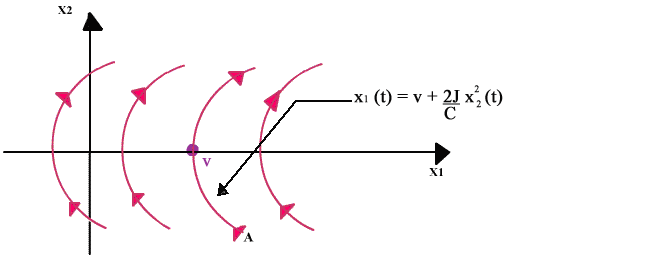
corrispondenti traiettorie
sono delle parabole come mostrato in figura.
Una di queste parabole di equazione è
particolarmente interessante perché passa per lo stato x*
che si vuol raggiungere. La parabola che passa per il punto A e per il
punto x* è certamente una traiettoria ottima perché
trasferisce il sistema da A a x* accelerando al massimo.
Similmente
per
si ottengono altre parabole (vedi figura) tra cui è di interesse
quella di equazioneperché
anch’essa rappresenta la traiettoria ottima da B a x* (massima decelerazione).
Quanto finora ottenuto si
può riassumere dicendo che se lo stato del sistema è su uno
dei due rami parabolici della funzione la
variabile d'ingresso deve essere pari a la
coppia u(t) deve essere pari a -C perché l’antenna va prima rallentata
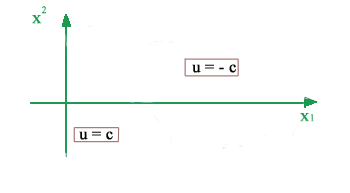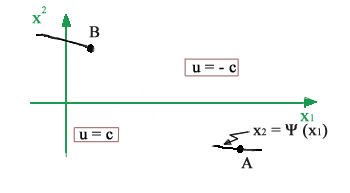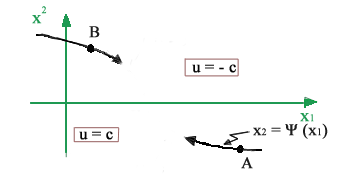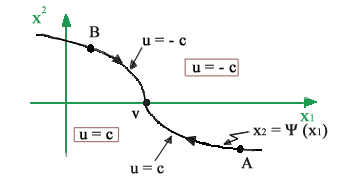
(frenando al massimo) finché si perviene ad un punto della curva
(vedi traiettoria OA di figura) ove si commuta passando ad u = C.
Viceversa, se lo stato x(t) del sistema corrisponde ad un punto che sta sotto la curva di figura, cioè se la
coppia u(t) deve essere pari a C finché si raggiunge il punto B
ove si commuta a u = -C.
In
conclusione, la legge di controllo è così definita
e lo schema di puntamento in tempo minimo è riassunto dallo schema a blocchi riportato in figura. |
rappresentata in figura.
(a seconda che ci si trovi in punti A o B) così che lo stato x*
venga raggiunto in tempo minimo. Se lo stato del sistema corrisponde invece
ad un punto che sta sopra la curva di figura, cioè se
