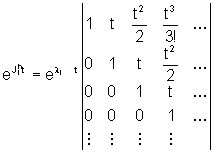| .Il problema della stabilità
può essere completamente risolto facendo riferimento alla forma
canonica di Jordan
Aj della matrice A. Più
precisamente, per mezzo di un opportuno cambiamento delle variabili di
stato
z=Tjx
è possibile trasformare il sistema assegnato
(A,b,cT,d) in un sistema equivalente
(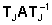 ,Tjb, ,Tjb,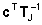 ,d)
in cui la matrice ,d)
in cui la matrice 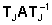 è la matrice di Jordan Aj. Il movimento
libero del sistema è allora descritto dalle equazioni
è la matrice di Jordan Aj. Il movimento
libero del sistema è allora descritto dalle equazioni
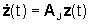
nel caso il sistema sia a tempo continuo, e dalle
equazioni
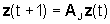
se il tempo è discreto. Il vantaggio di questa
trasformazione è che, a causa della struttura della matrice Aj,
il sistema risulta scomposto in tanti sottosistemi tra loro non interagenti,
uno per ogni miniblocco di Jordan
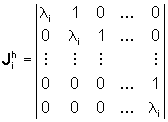
dove li
è
l'i-esimo autovalore distinto della matrice A e 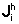 ha dimensioni
ha dimensioni 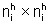 con
con 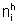 minore
o uguale alla molteplicità dell'autovalore linel
polinomio minimo yA(l).
Nel caso di sistemi a tempo continuo, la matrice di transizione di ognuno
di questi sottosistemi è allora minore
o uguale alla molteplicità dell'autovalore linel
polinomio minimo yA(l).
Nel caso di sistemi a tempo continuo, la matrice di transizione di ognuno
di questi sottosistemi è allora
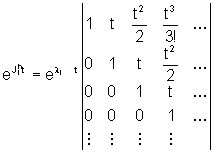
e contiene, quindi, termini del tipo 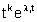 con k minore della molteplicità dell'autovalore linel
polinomio minimo yA(l).
Poiché
con k minore della molteplicità dell'autovalore linel
polinomio minimo yA(l).
Poiché 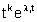 tende a zero per
tende a zero per 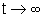 se e solo se la parte reale di liè
negativa, segue che un sistema a tempo continuo è asintoticamente
stabile se e solo se tutti gli autovalori di A hanno parte reale
negativa. Se esistono autovalori con parte reale positiva, alcuni termini
della matrice di transizione sono illimitati e crescono con legge esponenziale
(k=0) o più che esponenziale (
se e solo se la parte reale di liè
negativa, segue che un sistema a tempo continuo è asintoticamente
stabile se e solo se tutti gli autovalori di A hanno parte reale
negativa. Se esistono autovalori con parte reale positiva, alcuni termini
della matrice di transizione sono illimitati e crescono con legge esponenziale
(k=0) o più che esponenziale (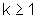 ).
È questo il caso dell'instabilità forte. Nei casi rimanenti,
cioè nei casi in cui esistono autovalori nulli o immaginari, ma
non esistono autovalori con parte reale positiva, si ha semplice stabilità
se il termine ).
È questo il caso dell'instabilità forte. Nei casi rimanenti,
cioè nei casi in cui esistono autovalori nulli o immaginari, ma
non esistono autovalori con parte reale positiva, si ha semplice stabilità
se il termine 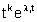 è limitato (k=0) e instabilità debole nel caso opposto (
è limitato (k=0) e instabilità debole nel caso opposto (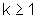 ).
Tenendo conto che k è forzatamente nullo solo nel caso in cui l'autovalore
a parte reale nulla è radice semplice del polinomio minimoyA(l)
e osservando che nel caso dei sistemi a tempo discreto l'esponenziale ).
Tenendo conto che k è forzatamente nullo solo nel caso in cui l'autovalore
a parte reale nulla è radice semplice del polinomio minimoyA(l)
e osservando che nel caso dei sistemi a tempo discreto l'esponenziale 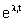 è sostituito dalla potenza
è sostituito dalla potenza 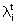 (che tende a zero se e solo se
(che tende a zero se e solo se 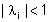 )
si può riassumere quanto detto con il seguente quadro di condizioni. )
si può riassumere quanto detto con il seguente quadro di condizioni.

Un sistema lineare (A,b,cT,d)
a tempo continuo [discreto] è
| (i) asintoticamente stabile se e solo
se |
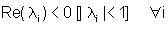 |
| (ii) semplicemente stabile
se e solo se |
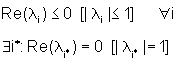
tutti i 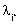 sono radici semplici di yA
sono radici semplici di yA |
| (iii) debolmente
instabile se e solo se |
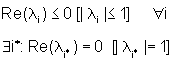
almeno un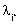 non
è radice semplice di yA non
è radice semplice di yA |
| (iv) fortemente instabile se e solo se |
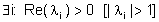 |
|
Il sistema che rappresenta la legge di Newton
(Esempio 1) (che ha la matrice A in forma di Jordan) ha un
autovalore nullo che è radice doppia del polinomio minimo. Come
già detto, esso è, pertanto, debolmente instabile. Il sistema
di Fibonacci (Esempio 2) ha, invece, due autovalori 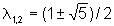 per cui uno dei due autovalori è maggiore di 1 e il sistema è,
quindi, fortemente instabile.
per cui uno dei due autovalori è maggiore di 1 e il sistema è,
quindi, fortemente instabile.
Gli n autovalori della matrice A
di un sistema lineare a tempo continuo possono essere raggruppati in tre
classi a seconda del segno della loro parte reale: n- autovalori
(detti stabili) hanno parte reale negativa, n0 hanno parte reale
nulla ( e sono detti critici) e n+ hanno parte reale positiva
(e sono detti instabili). Ovviamente n=n-+n0+n+.
I corrispondenti autovettori individuano tre sottospazi invarianti e disgiunti
X-,
X0
e X+ di dimensioni n-, n0 e n+.
Stati iniziali nel sottospazio
X- danno luogo a movimenti
liberi che tendono a zero, mentre stati iniziali nel sottospazio X+
danno luogo a movimenti illimitati. Per questo motivo, questi due sottospazi
si chiamano, rispettivamente,
varietà stabile e varietà
instabile. Il sottospazio
X0 si chiama, invece, varietà
centro: i movimenti liberi corrispondenti a stati iniziali appartenenti
a X0 danno luogo a traiettorie limitate che restano in
X0
ma non tendono a zero. Sistemi senza varietà centro (cioè
senza autovalori critici) si chiamano iperbolici e sono distinti
in attrattori (X-=Rn),
selle
(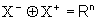 ) e repulsori
(X+=Rn). Sistemi con varietà centro
si chiamano, invece, non iperbolici. In Fig. 9 sono mostrate
le traiettorie corrispondenti al movimento libero di otto diversi sistemi
del secondo ordine a tempo continuo. In ogni figura sono mostrati anche
i due autovalori del sistema. I primi cinque sistemi (fuoco stabile, nodo
stabile, fuoco instabile, nodo instabile, sella) sono iperbolici e gli
ultimi tre non iperbolici. L'ultimo sistema (autovalori immaginari) si
chiama centro e giustifica il termine "varietà centro". ) e repulsori
(X+=Rn). Sistemi con varietà centro
si chiamano, invece, non iperbolici. In Fig. 9 sono mostrate
le traiettorie corrispondenti al movimento libero di otto diversi sistemi
del secondo ordine a tempo continuo. In ogni figura sono mostrati anche
i due autovalori del sistema. I primi cinque sistemi (fuoco stabile, nodo
stabile, fuoco instabile, nodo instabile, sella) sono iperbolici e gli
ultimi tre non iperbolici. L'ultimo sistema (autovalori immaginari) si
chiama centro e giustifica il termine "varietà centro".
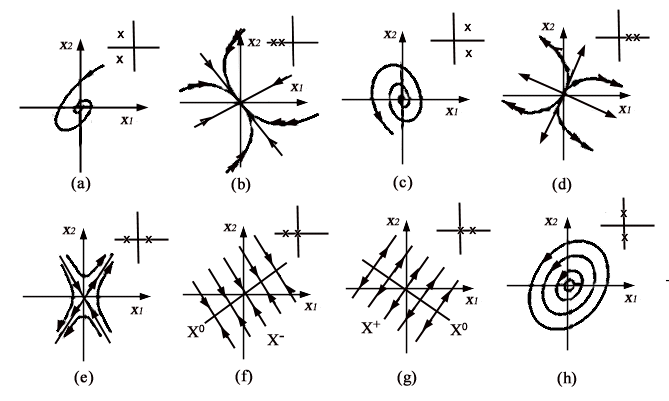
|
Figura 9 Traiettorie
corrispondenti al movimento libero di sistemi del secondo ordine a tempo
continuo: (a) (fuoco stabile) e
(b) (nodo stabile) sono
attrattori; (c) (fuoco instabile) e (d) (nodo instabile) sono repulsori;
(e) è una sella; (f), (g) e (h) (centro) sono sistemi con varietà
centro
X0.
Le traiettorie rettilinee
corrispondono ad autovettori associati ad autovalori reali. La doppia freccia
indica parti delle traiettorie percorse più rapidamente. |
Il vantaggio della scomposizione dello
spazio di stato Rn nella somma diretta dei tre sottospazi X-,
X0
e X+ è particolarmente utile per visualizzare
la geometria del movimento libero, in particolare in sistemi del terzo
ordine, come le due selle mostrate in Fig. 10.
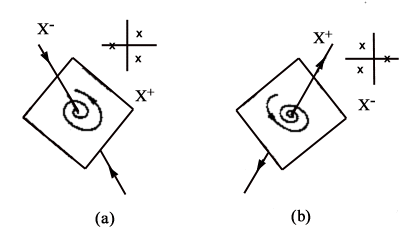
|
|
Figura 10 Due
selle del terzo ordine: (a) n-=1, n+=2; (b) n-=2,
n+=1
|
Naturalmente, quanto detto per i sistemi
a tempo continuo vale anche per quelli a tempo discreto, pur di discriminare
tra autovalori stabili (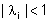 ),
critici ( ),
critici (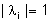 ) e
instabili ( ) e
instabili (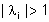 ). ). |