L'osservabilità di un sistema dinamico è una proprietà che ha a che fare con la possibilità di risolvere un problema "inverso", quello del calcolo dello stato iniziale x(0) a partire dalla conoscenza delle funzioni di ingresso e uscita nell'intervallo di tempo [0,t). Analogamente, la ricostruibilità ha a che fare con la possibilità di calcolare lo stato finale x(t). È ovvio, pertanto, che l'osservabilità implica la ricostruibilità, perché noti x(0) e u[0,t)(.) è possibile calcolare x(t) (formula di Lagrange), mentre l'inverso è vero se il sistema è reversibile.

Per analizzare la tematica dell'osservabilità è opportuno considerare il movimento libero del sistema

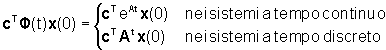
e definire l'insieme Xno(t) degli stati indistinguibili dall'origine come l'insieme degli stati iniziali x(0) per i quali il movimento libero è identicamente nullo nell'intervallo [0,t). Evidentemente, tale insieme è un sottospazio che gode della proprietà

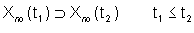
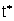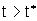Inoltre, si può mostrare che Xno(t) smette di decrescere a partire da un certo istante , cioé Xno(t)= Xno per . Infine, se 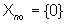, il sistema non ha stati indistinguibili dall'origine e si può mostrare che questa condizione è necessaria e sufficiente per la completa osservabilità del sistema nell'intervallo 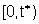, cioé per la possibilità di calcolare x(0) da u[0,t)(.) e y[0,t)(.). In questo contesto è anche utile far ricorso al sottospazio 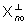 cioé al sottospazio complementare e ortogonale a Xno. Tale sottospazio, chiamato sottospazio di osservabilità e indicato con Xo, è spesso utile per formulare esplicitamente la condizione di completa osservabilità.


 
In un sistema lineare di ordine n il sottospazio di osservabilità Xo è individuato dagli n vettori 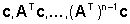, detti vettori di osservabilità. Il sistema è, pertanto, completamente osservabile se e solo se tali vettori sono linearmente indipendenti. Inoltre, in un sistema completamente osservabile, lo stato iniziale può essere calcolato se le funzioni di ingresso e uscita sono note su un intervallo di tempo di durata qualsiasi se il sistema è a tempo continuo e di durata al più pari a n se il sistema è a tempo discreto.
La condizione appena vista è spesso formulata facendo riferimento alla matrice di osservabilità (detta anche matrice di Kalman)

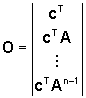
che ha le righe costituite dai vettori di osservabilità (trasposti). Per quanto detto, si ha

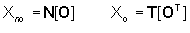e un sistema è completamente osservabile se la sua matrice di osservabilità è non singolare (cioè se esiste la matrice O-1). Questa condizione è facilmente verificabile nei sistemi a tempo discreto, nei quali

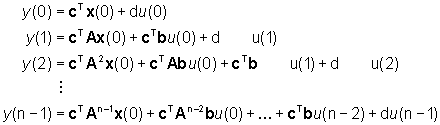
Infatti, il sistema appena scritto, che ha n equazioni e n incognite (il vettore x(0), è risolubile se e solo se la matrice di osservabilità O è non singolare.


Il confronto dei Teoremi 12 e 15 permette di notare una forte analogia tra raggiungibilità e osservabilità, formalizzabile nel seguente principio di dualità.


 
Indicato come duale del sistema  il sistema , si può affermare che un sistema S è completamente raggiungibile [osservabile] se e solo se il suo duale  è completamente osservabile [raggiungibile]. Inoltre, la matrice di raggiungibilità di un sistema è la trasposta della matrice di osservabilità del sistema duale.
Tale principio permette di ricavare immediatamente dal Teorema 13 e dalle proprietà della forma canonica di controllo il seguente risultato.

 
Un sistema in forma canonica di ricostruzione

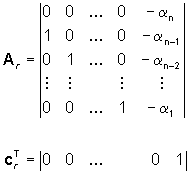
è completamente osservabile. Viceversa, un sistema (A,cT) completamente osservabile può essere messo in forma canonica di ricostruzione per mezzo di una opportuna trasformazione di coordinate.

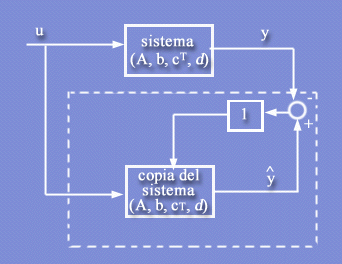
Anche il Teorema 14 sull'equivalenza tra completa raggiungibilità e fissabilità degli autovalori del sistema controllato può essere dualizzato. Per questo premettiamo la nozione di ricostruttore dello stato, illustrata schematicamente in Fig. 14.
 
Figura 14 Un sistema con ricostruttore dello stato

Il ricostruttore è costituito da una copia del sistema (con stato 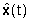) cui è, tuttavia, applicato, oltre all'ingresso u(t), un secondo ingresso (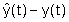) legato alla differenza tra l'uscita ricostruita 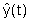 e l'uscita del sistema. Il vettore l, che identifica univocamente il ricostruttore, verrà supposto, d'ora in avanti, costante nel tempo (ricostruttore invariante). Come vedremo tra poco, ciò equivale, in generale, a rinunciare alla possibilità di ricostruire esattamente lo stato del sistema in tempo finito. D'altra parte, la sintesi dei ricostruttori varianti è decisamente più complicata di quella qui trattata dei ricostruttori invarianti. Se il sistema è, ad esempio, a tempo continuo, per cui

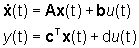
il suo ricostruttore invariante è, allora, descritto dalle equazioni

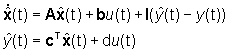
Indicato con

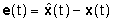
l'errore di ricostruzione, cioè la differenza tra stato 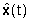 del ricostruttore e stato x(t) del sistema, è immediato verificare che

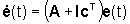          (27')

Ciò significa che la dinamica dell'errore di ricostruzione è la dinamica del sistema libero (27') con stato iniziale 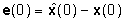, e non risente, quindi, in alcun modo dell'ingresso applicato al sistema. Nel caso di sistemi a tempo discreto la (27') diventa semplicemente
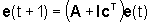       (27'')

per cui si può concludere che lo stato ricostruito 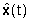 tende allo stato del sistema x(t), qualsiasi sia l'errore di stima iniziale , se e solo se il sistema (27) è asintoticamente stabile. Quando ciò si verifica si dice che il ricostruttore l è un ricostruttore asintotico dello stato. Naturalmente, la velocità con cui lo stato ricostruito 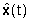 converge verso x(t) è legata agli autovalori (e, in particolare, all'autovalore dominante) della matrice 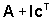. A questo proposito è interessante tener presente il seguente risultato, che è, appunto, il duale di quello sulla fissabilità degli autovalori del sistema controllato.


 
Gli autovalori della matrice 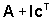 (che descrive la dinamica dell'errore di ricostruzione (27)) possono essere fissati arbitrariamente per mezzo di un ricostruttore l, se e solo se il sistema (A,cT) è completamente osservabile.
Questo risultato dice che elaborando in tempo reale le misure d'ingresso e uscita di un sistema lineare completamente osservabile è possibile ricostruire con grande rapidità e precisione lo stato del sistema. Poiché la completa osservabilità è (come la completa raggiungibilità) una proprietà genericamente soddisfatta in un sistema lineare, si può capire come lo schema di Fig. 14 sia di grande interesse nelle applicazioni.

 
Indietro  Avanti