Le nozioni di raggiungibilità e osservabilità permettono di interpretare un qualsiasi sistema lineare come l'aggregato di quattro sottosistemi chiamati, rispettivamente,
(a) parte raggiungibile e non osservabile (r,no)
(b) parte raggiungibile e osservabile (r,o)
(c) parte non raggiungibile e non osservabile (nr,no)
(d) parte non raggiungibile e osservabile (nr,o)
Se la dimensione del sistema è n e na, nb, nc e nd sono le dimensioni delle quattro parti, ovviamente

n=na+nb+nc+nd

Solo raramente un sistema è costituito da tutte e quattro le parti, anzi, frequente è il caso in cui un sistema è costituito dalla sola parte (b): ciò accade quando il sistema è completamente raggiungibile e completamente osservabile. Le interazioni tra i quattro sottosistemi Sa ,Sb, Sc e Sd sono rappresentate nello schema di Fig. 15 in cui, per semplicità, si è supposto che il sistema sia proprio (d=0).
 

Figura 15 Un sistema proprio scomposto in parti

La figura mostra che l'ingresso u influenza direttamente le parti (a) e (b) e non influenza invece, neppure indirettamente, le parti (c) e (d). Ciò significa che se i sottosistemi (c) e (d) sono inizialmente a riposo () essi resteranno tali, qualsiasi sia l'azione esercitata dall'esterno sul sistema. Al contrario, i vettori di stato za e zb delle prime due parti potranno essere fatti variare, perché influenzati dall'ingresso. Anzi, il teorema di scomposizione (dovuto a Kalman), che vedremo tra poco, precisa che il sistema costituito dalle prime due parti è completamente raggiungibile. La figura mostra anche che l'uscita risente dell'ingresso del sistema soltanto attraverso la parte (b), che è, quindi, l'unica vera responsabile dell'elaborazione di informazione che avviene tra ingresso e uscita di un sistema dinamico. L'uscita è anche influenzata dalla parte (d) ed è, invece, completamente insensibile a ciò che avviene nelle parti (a) e (c): ciò significa che non sarà possibile calcolare lo stato iniziale delle parti (a) e (c) a partire da registrazioni di ingresso e uscita. Al contrario, ciò è possibile, come è precisato dal teorema che segue, per le parti (b) e (d) che costituiscono un sistema completamente osservabile.


 
Dato un sistema lineare  è possibile effettuare un cambiamento di variabili di stato z=Tx in modo tale che il sistema equivalente  sia scomposto in parti (come mostrato in Fig. 15), cioè

Inoltre, il sistema  è completamente raggiungibile e osservabile, mentre il sistema  dato da

è completamente raggiungibile e il sistema  dato da

è completamente osservabile.
La dimostrazione di questo teorema è costruttiva perché suggerisce la seguente procedura per il calcolo della matrice T che individua il cambiamento di coordinate voluto.

1. Si calcolino le matrici di raggiungibilità R e di osservabilità O del sistema 
2. Si determinino i quattro sottospazi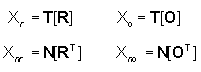
3. Si determinino i quattro sottospazi (e una loro base)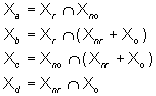


4. Si costruisca una matrice T-1 che abbia come colonne i vettori costituenti le basi dei quattro sottospazi di cui al punto precedente e, quindi, si calcoli T.
5. Si determini la terna .
È importante notare che le quattro parti costituenti un sistema lineare, benché tra loro interconnesse, non formano cicli, come evidente sia dalla Fig. 15 che dalla struttura (triangolare a blocchi) della matrice TAT-1. Ciò implica che gli autovalori del sistema siano semplicemente la riunione degli autovalori delle quattro parti o, equivalentemente, che il polinomio caratteristico del sistema sia il prodotto dei polinomi caratteristici delle quattro parti. Per questo motivo, molte proprietà di un sistema lineare sono, in ultima analisi, legate alle proprietà di stabilità di una o più delle sue parti. A questo proposito, discutiamo qui di seguito tre proprietà dei sistemi lineari: stabilizzabilità, rivelabilità ed esterna stabilità.
La prima proprietà, la stabilizzabilità, altro non è che la possibilità di trasformare un sistema assegnato (A,b,cT,d) in un sistema asintoticamente stabile, asservendone l'ingresso allo stato per mezzo di una legge di controllo lineare. Immaginando che il sistema sia scomposto nelle sue quattro parti con stato za, zb, zc e zd, ciò equivale a supporre che

È chiaro, anche solo guardando la Fig. 15, che questa operazione non modifica la dinamica delle parti (c) e (d), i cui autovalori restano, quindi, autovalori del sistema controllato. Perché il sistema (A,b,cT,d) sia stabilizzabile è quindi necessario che le parti (c) e(d) siano asintoticamente stabili. Ma, d'altra parte, questa condizione è anche sufficiente, perché, per il Teorema 14, i rimanenti autovalori possono essere modificati a piacere, dato che le parti (a) e (b) costituiscono un sistema completamente raggiungibile. In conclusione, quindi, vale il seguente risultato.


 
Un sistema è stabilizzabile se e solo se le sue parti non raggiungibili ((c) e (d)) sono asintoticamente stabili.
Un risultato duale vale per la cosiddetta rivelabilità, cioè per la possibilità di ricostruire, almeno asintoticamente, lo stato di un sistema per mezzo di un ricostruttore lineare e invariante.

 
Un sistema è rivelabile se e solo se le sue parti non osservabili ((a) e (c)) sono asintoticamente stabili.
Anche questo risultato è intuibile per semplice ispezione della Fig. 15. Infatti, poiché le parti (b) e (d) costituiscono un sistema completamente osservabile, il loro stato zb(t) e zd(t) può essere determinato con grande precisione elaborando ingresso e uscita per mezzo di un ricostruttore (si veda il Teorema 18). Ma, allora, gli ingressi u(T), zb(t) e zd(t) del sistema costituito dalle parti (a) e (c) sono noti, per cui il movimento forzato di tale sistema può essere calcolato. Ma, se le parti (a) e (c) sono asintoticamente stabili, il movimento forzato approssima sempre di più, al passare del tempo, lo stato za(t) e zc(t) di queste due parti, per cui, in conclusione, il sistema è rivelabile.

Decisamente più importante delle due precedenti è la proprietà di esterna stabilità (nota anche come stabilità BIBO dall'inglese Bounded Input Bounded Output) di cui diamo la definizione formale.


 
Un sistema lineare è esternamente stabile se e solo se la sua uscita forzata è limitata per ogni ingresso limitato.
Facendo riferimento, una volta di più, allo schema di Fig. 15, ci si rende immediatamente conto che la stabilità esterna è una proprietà della sola parte (b) del sistema perché il movimento libero è caratterizzato da  e  e la parte (a) non dà alcun contributo all'uscita. Non sorprende, quindi, che la stabilità esterna di un sistema sia legata all'asintotica stabilità della sua parte (b).

 
Un sistema è esternamente stabile se e solo se la sua parte raggiungibile e osservabile è asintoticamente stabile.
Questo risultato è dovuto al fatto che solo la parte (b) è responsabile delle relazioni intercorrenti tra ingresso e uscita qualora lo stato iniziale sia nullo. Nel caso, invece, lo stato iniziale non sia nullo, l'uscita risente anche del contributo della parte (d), contributo che è però, per definizione, limitato se tale parte è stabile (semplicemente o asintoticamente). Si può così concludere che l'uscita di un sistema è limitata per qualsiasi stato iniziale e qualsiasi ingresso limitato se e solo se la sua parte raggiungibile e osservabile (b) è asintoticamente stabile e la sua parte non raggiungibibile e osservabile (d) è stabile.

 
Indietro  Avanti