| Avendo dato due diverse definizioni
di sistema dinamico (una interna
e una esterna)
è importante capire come si possa passare da una descrizione all'altra.
Il problema del calcolo delle relazioni ingresso-uscita (cioè del modello ARMA e della funzione di trasferimento) di un sistema assegnato mediante una quaterna (A,b,cT,d) può essere ben inquadrato soltanto dopo aver introdotto le nozioni di raggiungibilità e osservabilità. Per ora notiamo che le (1) e (3), ricordando il significato dell'operatore p, possono essere scritte nella forma
per cui  Dalle (2) e (4) segue allora che  e un confronto con le (7) e (8) fornisce 
(12)Per l'inversione della matrice (pI-A)
di dimensioni  dove P(p) è una matrice 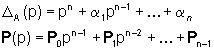 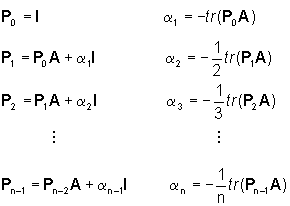 Se, a conti fatti, la funzione di trasferimento G(p)=n(p)/d(p) ha il polinomio d(p) di grado n, allora dalle formule di Souriau segue che d(p)=D(p)=DA(p) cioé il modello ARMA (N(p),D(p)) del sistema è in forma ridotta ed è, quindi, deducibile dalla funzione di trasferimento. Inoltre, sempre nel caso di modello ARMA ridotto, i poli della funzione di trasferimento sono n e coincidono con gli autovalori della matrice A. Nal caso, invece, il modello ARMA non sia in forma ridotta, i poli della funzione di trasferimento sono meno di n, ma coincidono sempre con alcuni degli autovalori della matrice A. Il problema della determinazione di una quaterna (A,b,cT,d) che abbia come modello ARMA un modello (N(p),D(p)) assegnato è noto come problema della realizzazione (con lo stesso nome si indica anche la quaterna (A,b, cT,d) che risolve il problema). La soluzione di questo problema non è unica, per cui risulta di particolare interesse determinare la realizzazione di ordine minimo. Per affrontare questo tema è, tuttavia, necessario aver approfondito le nozioni di raggiungibilità e osservabilità. Per ora accontentiamoci di affermare (la dimostrazione non è immediata) che una particolare realizzazione, detta in forma canonica di controllo, di un assegnato modello ARMA (anche non ridotto) 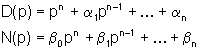 è la quaterna 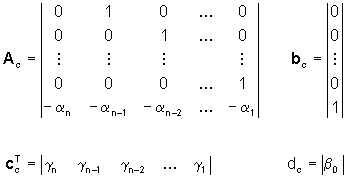 con
gi=bi-b0ai i=1,…,n La realizzazione in forma canonica di controllo
è un sistema di ordine (n) pari alla "dimensione" della parte autoregressiva
del modello ARMA.
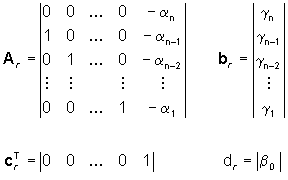 È opportuno notare che
perché su questa formula torneremo quando parleremo del principio di dualità.
|
Indietro |
Avanti  |
,
si può procedere nel modo seguente (metodo di Souriau). Posta
la matrice (pI-A)-1 nella forma
