Aggregati di sottosistemi e formula di Mason

Spesso alcuni sistemi dinamici interagiscono tra loro e l'aggregato che così si ottiene è, pur esso, un sistema dinamico. Due sistemi dinamici S₁e S₂possono essere collegati in tre modi: cascata, parallelo e retroazione. Per questo dobbiamo tener conto che se x⁽¹⁾ e x⁽²⁾sono i vettori di stato diS₁ e S_2, il vettore di stato x diS sarà

. In particolare, detti

i=1,2, i due sottosistemi, siamo interessati a determinare il sistema aggregato S=(A,b,c^T,d).

Due sistemi sono collegati in cascata (Fig. 3) quando l'uscita del primo sistema è l'ingresso del secondo.

Figura 3 Due sistemi collegati in cascata

Le equazioni di stato di S sono pertanto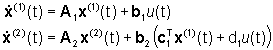

mentre la trasformazione di uscita è data da

In conclusione, S è individuato dalla seguente quaterna

Si noti che la matrice A è triangolare a blocchi, per cui i suoi autovalori sono quelli delle matrici A₁ e A₂.

Due sistemi sono collegati in parallelo (Fig. 4) quando hanno l'ingresso in comune e le loro uscite si sommano.

Figura 4 Due sistemi collegati in parallelo

È immediato verificare che l'aggregato S è individuato dalle seguenti quattro matrici

Anche in questo caso la matrice A è triangolare (anzi diagonale) a blocchi così che i suoi autovalori sono quelli delle matrici A₁ e A_2.

Due sistemi sono collegati in retroazione (Fig. 5) quando l'ingresso del primo è la somma di un ingresso esterno u e dell'uscita del secondo e l'ingresso del secondo è l'uscita del primo.

Figura 5 Due sistemi collegati in retroazione
(S₁ è in linea di andata e S₂ in linea di retroazione)

Naturalmente gli aggregati di sottosistemi possono anche essere studiati dal punto di vista esterno. Anzi, il modello ARMA e la funzione di trasferimento di S sono facilmente determinabili a partire dai modelli ARMA e dalle funzioni di trasferimento di tutti i sottosistemi. Per renderci conto di ciò, analizziamo innanzitutto il caso dei collegamenti in cascata, parallelo e retroazione di due sottosistemi.

Con riferimento alla Fig. 3 supponiamo che S₁=(N1(p),D1(p)) eS₂=(N2(p),D2(p)). Ciò significa che il modello ARMA del primo sottosistema è D₁(p)y⁽¹⁾(t)=N₁(p)u(t)

Applicando, allora, a entrambi i membri di questa relazione l'operatore N2(p) e notando che y⁽¹⁾=u⁽²⁾ otteniamo

N₂(p)D₁(p)u⁽²⁾(t)= N₂(p)N₁(p)u(t)

Ma (anche in termini operatoriali) N₂D₁=D₁N₂e N₂N₁=N₁N₂ perché derivare (o anticipare) una funzione prima r volte e poi s volte è equivalente a derivarla (o anticiparla) prima s volte e poi r volte, per cui si può scrivere

D₁(p)N₂(p)u⁽²⁾(t)= N₁(p)N₂(p)u(t)

D'altra parte, la relazione ARMA del secondo sottosistema è

D₂(p)y(t)= N₂(p)u⁽²⁾(t)

per cui, in definitiva, si ottiene

D₁(p)D₂(p)y(t) = N₁(p)N₂(p)u(t)

In altre parole, se due sistemi S₁eS₂sono collegati in cascata, il sistema risultante Sè caratterizzato da un modello ARMA individuato dai seguenti due polinomi

N(p)=N₁(p)N₂(p) D(p)=D₁(p)D₂(p)

Ciò significa che la funzione di trasferimento G(p)=N(p)/D(p) di S si ottiene moltiplicando tra loro le due funzioni di trasferimento G₁(p) e G₂(p) dei due sottosistemi, cioè

G(p)=G₁(p)G₂(p)

Questo risultato permette di concludere che l'ordine secondo cui i due sottosistemi vengono disposti in cascata non influenza la funzione di trasferimento dell'aggregato.

Facendo riferimento alla Fig. 4 e procedendo come nel caso del collegamento in cascata è facile dimostrare che la funzione di trasferimento di S è G(p)=G₁(p)+G₂(p)

In altre parole, la funzione di trasferimento di un sistema costituito da due sottosistemi collegati in parallelo è la somma delle due funzioni di trasferimento.

Nel caso di due sistemi S₁ e S₂ collegati in retroazione come mostrato in Fig. 5 si perviene, invece, alla formula

Questa formula, utilissima per l'analisi dei sistemi retroazionati, vale per il collegamento mostrato in Fig. 5 in cui la retroazione è detta positiva perché il segnale y⁽²⁾ proveniente dalla retroazione viene sommato al segnale esterno u. Nel caso si faccia, invece, riferimento ad uno schema con retroazione negativa

u⁽¹⁾=u-y⁽²⁾

la formula da usare risulta ovviamente

Tale formula viene spesso enunciata a parole, dicendo che la funzione di trasferimento di un sistema retroazionato negativamente è il rapporto tra la funzione di trasferimento in linea di andata (G₁) e la funzione di trasferimento d'anello (G₁G₂) aumentata dell'unità. Chiamare funzione di trasferimento d'anello la funzione G₁G₂ è pienamente giustificato, dato che nell'anello i due sistemi S₁ e S₂ sono in cascata l'uno all'altro.

La formula di Mason generalizza quanto appena visto e permette di calcolare la funzione di trasferimento G(p) di un qualsiasi aggregato di sottosistemi. Nell'ipotesi che nello schema che definisce l'aggregato siano usati solo nodi sommatori (cioè nell'ipotesi che nell'aggregato vengano soltanto effettuate somme tra segnali) la formula è la seguente

dove C_k(p), D(p) e D_k(p) si chiamano, rispettivamente, funzione di trasferimento del k-esimo cammino diretto (cioè non contenente cicli) tra ingresso e uscita, determinante dell'aggregato, e determinante ridotto rispetto al k-esimo cammino diretto. La funzione di trasferimento C_k(p)è semplicemente il prodotto delle funzioni di trasferimento di tutti i sistemi che costituiscono il k-esimo cammino diretto. Il determinante D(p) è, invece, dato da

dove L_i(p) è la funzione di trasferimento dell'i-esimo cammino chiuso (anello), cioè il prodotto delle funzioni di trasferimento di tutti i sistemi che costituiscono l'i-esimo percorso chiuso esistente nell'aggregato. Nella formula, la prima sommatoria è estesa a tutti gli anelli, la seconda alle coppie di anelli disgiunti (cioè che non si toccano) e così via. Infine, il determinante ridotto D_kè il determinante privato di tutti i termini relativi ad anelli non disgiunti (cioè toccati) dal k-esimo cammino diretto. In alcuni casi può non essere facile individuare tutti i percorsi diretti e tutti gli anelli per ispezione del grafo rappresentante l'aggregato (usualmente chiamato schema a blocchi). In molti casi di interesse pratico, l'applicazione della formula di Mason è tuttavia immediata, soprattutto qualora non esistano anelli disgiunti.

Indietro

Avanti