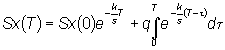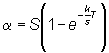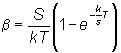Ricostruzione di dati idrologici mancanti: SOLUZIONE
L'intero bacino può essere modellizzato per mezzo di un sistema lineare a tempo discreto in cui l'ingresso è l'afflusso totale dovuto alla precipitazione e l'uscita è il deflusso giornaliero dell'emissario del lago più a valle. 
La ricostruzione delle precipitazioni dai dati di deflusso è quindi un problema (inverso) di ricostruzione degli ingressi dalle uscite. Tale problema è risolubile se il sistema è a sfasamento minimo, cioè se gli zeri della funzione di trasferimento sono minori di uno in modulo.
 

IL MODELLO: 
Indicato con x(t) il livello di un lago, misurato rispetto al fondo dell'emissario, e con q(t) e kx(t) le portate volumetriche di ingresso e uscita, il principio di conservazione della massa fornisce l'equazione:
 

(1)

Supponendo:

q(t)= q = costante

durante la giornata ( ) si ottiene (si ricordi la formula di Lagrange):

 
Indicato con t = 0, 1, 2,... il giorno, con x(t) il livello del lago all'inizio del giorno t e con v(t) l'afflusso volumetrico durante il giorno t (pari a q.T), la (1) può essere riscritta, genericamente, come:
 
(2)

con :
 

(3)

Indicato con u(t) l'afflusso volumetrico giornaliero dovuto alla precipitazione su tutto il territorio in esame e con xi(t) il livello dell'i-esimo lago, la (2) può allora essere scritta per ognuno dei cinque laghi:
 

Il bacino è quindi descritto dal sistema lineare a tempo discreto:
 
 

con:
 

dove i parametri a e b sono facilmente calcolabili dai dati con le (3).

 
RICOSTRUIBILITA' DEGLI INGRESSI E DELLE USCITE:
Gli ingressi u(t) di un sistema lineare sono ricostruibili dalle uscite se e solo se il sistema è a sfasamento minimo, cioè se e solo se gli zeri della funzione di trasferimento
 

sono minori di uno in modulo. Per sapere se le precipitazioni giornaliere sul bacino sono ricostruibili dai dati di deflusso è pertanto sufficiente calcolare gli zeri della funzione di trasferimento, cosa che risulta, ovviamente, facilitata qualora si disponga di un package per l'analisi strutturale dei sistemi lineari.

CALCOLO DELLE PRECIPITAZIONI: 
Per calcolare le precipitazioni u(t) si può usare il modello ARMA:
 
(4)

che interpreta, nel dominio del tempo, la funzione di trasferimento:
 

Risolvendo la (4) rispetto a u(t-1) (supponendo che nel caso specifico sia b1 diverso da zero), si ottiene una relazione esplicita per la stima dell'afflusso  nel giorno (t-1), basata sulle stime degli afflussi nei giorni (t-2), (t-3), (t-4) e (t-5) e sui deflussi nei giorni t, (t-1),...,(t-5):
 

Tale relazione può essere usata recursivamente incrementando t e usando le misure di deflusso y. Naturalmente per inizializzare il calcolo è necessario fissare i primi quattro valori di afflusso, cosa che può essere fatta anche a caso dato che il metodo di  ricostruzione converge (cioè tende a u(t) per t che tende a infinito) indipendentemente dalle condizioni iniziali se il sistema è a sfasamento minimo. Anzi, la convergenza a zero dell'errore di stima è almeno rapida quanto |zmax|', essendo zmax lo zero più grande in modulo di G(z).
APPLICAZIONE PRECEDENTE
Testo
  APPLICAZIONE SUCCESSIVA