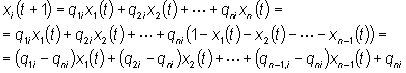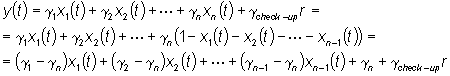Gestione di tre reti di calcolatori: SOLUZIONE
Il problema può essere risolto riconoscendo che il costo di gestione corrispondente ad ogni particolare politica di check-up può essere interpretato come l'uscita di un particolare sistema lineare a tempo discreto. 
La scelta della miglior politica di check-up è pertanto equivalente alla scelta del sistema a minimo guadagno in una classe assegnata di sistemi.
 

IL MODELLO: 
All'inizio di ogni settimana, il sistema complessivo formato dalle tre reti A, B e C può essere in uno dei seguenti otto stati: 
 

 
A
B
C
g
1
1
1
1
0
2
1
1
2
1
3
1
2
1
1
4
1
2
2
2
5
2
1
1
1
6
2
1
2
2
7
2
2
1
2
8
2
2
2
3

dove con g si è indicato il numero di reti guaste corrispondente ad ogni stato. 
Le probabilità di transizione  (i,j=1,2,...,8) tra questi stati dipendono dalla politica di check-up adottata, vale a dire dal numero r di reti sottoposte a check-up settimanale (r=0,1,2, o 3). 

Ad esempio, nel caso r=0 si ha:
 

.....
.....
.....
.....

Nel caso r=1 (supponendo sia la rete A quella sottoposta a check-up):
 

.....
.....
.....
.....

e analogamente per r=2 e 3. 
In questo modo, per ogni r fissato, il sistema è descritto da una catena di Markov (con n=8 stati) del tipo:
 

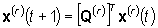(1)
dove  è il vettore delle probabilità di stato e la matrice  contiene le probabilità di transizione .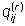 
Se indichiamo con 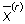 lo stato di equilibrio di questo sistema, il costo atteso (settimanale) di gestione 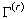 associato alla politica di check-up r è dato da:
 

dove giè il costo associato allo stato i (danno di mancato funzionamento + costo di riparazione), e gcheck-up è il costo relativo al check-up di una singola rete.

CALCOLO DEL COSTO DI GESTIONE:

Per calcolare il costo di gestione 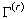 si può usare un package che determini la funzione di trasferimento del sistema lineare a tempo discreto che si ottiene eliminando una variabile (per esempio, la n-esima) nella (1). 
Infatti, per una particolare politica di check-up r, le prime (n-1) equazioni della catena di Markov si possono riscrivere nella forma (tralasciando l'apice (r) per semplicità):
 

con :
 

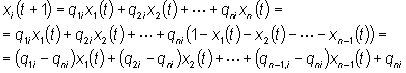i=1,2,…,n-1

mentre l'uscita y(t) (costo atteso) è data da:
 

Queste equazioni definiscono un sistema lineare a tempo discreto di ordine (n-1) del tipo:
 

che ha funzione di trasferimento:
 

Il costo di gestione G coincide con il guadagno del sistema, vale a dire:
 G= G(1).

DETERMINAZIONE DELLA POLITICA OTTIMA DI CHECK-UP:
Ad ogni politica di check-up r è associato un diverso sistema (A, b, cT, d)(r), e quindi un diverso costo di gestione G(r).
La politica di check-up ottima è, ovviamente, quella che rende minimo il costo di gestione G(r) e può pertanto essere facilmente determinata confrontando tra loro i guadagni G(1) delle funzioni di trasferimento dei sistemi associati ai quattro casi possibili r=0,1,2,3.

OSSERVAZIONE SULLA MINIMALITA':
Ci si può facilmente rendere conto che il sistema (A, b, cT, d) non è in forma minima (cioè non è completamente raggiungibile e osservabile). Ciò significa che il sistema può essere modellizzato con un numero inferiore di stati.
Infatti, gli stati caratterizzati dallo stesso numero di reti guaste (ad esempio gli stati 2, 3 e 5 che hanno g=1) sono del tutto equivalenti, cosicchè, per ogni politica di check-up r, il sistema informatico può essere modellizzato con una catena di Markov con 4 stati (g=0,1,2,3) anzichè 8. Ciò darebbe luogo ad una matrice A di dimensioni 3x3 e semplificherebbe pertanto il calcolo della funzione di trasferimento G(z) e del suo guadagno G(1).

APPLICAZIONE PRECEDENTE
Testo
  APPLICAZIONE SUCCESSIVA