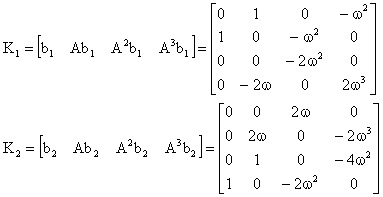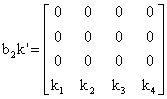|
Con
le ipotesi fatte il moto di una massa puntiforme è retto dalle due
seguenti equazioni
dove Se con
che
corrisponde ad un’orbita circolare di raggio R percorsa una volta ogni
Per
passare ad una descrizione in termini di variabili di stato si può
porre
da
cui, derivando e tenendo conto delle (1), si ottiene
Il
sistema non lineare (2) ammette l’origine come stato di equilibrio (tale
soluzione corrisponde fisicamente all’orbita circolare) e può essere,
pertanto, linearizzato intorno a tale stato di equilibrio. Le equazioni
(2.a) e (2.c) sono già lineari mentre le altre due possono essere
linearizzate trascurando i termini infinitesimi di ordine superiore al
primo (si ricordi che x1, x2, x3 e x4
sono infinitesimi del primo ordine). Per esempio per la (2.b) ottiene
ma
gli ultimi due termini hanno somma nulla e, quindi, alle piccole variazioni
Similmente,
si ottiene
e,
quindi, in conclusione il sistema linearizzato è del tipo
con
D'ora
in avanti per “sistema terra - satellite” si intenderà il sistema
(A, B, C) con A e B date dalla (3) e C uguale alla matrice unità
di ordine quattro, o uno qualsiasi dei sistemi ottenuti da questo considerando
uno solo dei due ingressi come ingresso e una sola delle variabili di stato
come uscita. Ad esempio, se si considera come solo ingresso la forza radiale
u1(t) e come uscita lo scostamento angolare x3(t)
si ottiene il sistema (A, b1, c3’) dato da
dato
da
dove
Perché
sia possibile determinare un regolatore con dinamica arbitraria è
necessario che il sistema sia completamente raggiungibile ed osservabile.
Pertanto, come primo passo ci si può chiedere se il sistema è
completamente raggiungibile con uno solo dei due ingressi o se necessita
entrambi gli ingressi. Per questo si considerano le due matrici di raggiungibilità
K1 e K2 dei sistemi (A, b1) e (A, b2).
Tali matrici sono date da
ed
è immediato verificare che K1 non è di rango massimo
(la seconda e la quarta colonna sono proporzionali) mentre K2
lo è. Ciò significa che agendo soltanto su u1
(spinta radiale) non si può variare lo stato del sistema a piacere,
mentre questo è possibile per mezzo del solo ingresso u2
(spinta tangenziale).
Pertanto,
allo scopo di controllare il satellite su un’orbita circolare si può
pensare di dotarlo soltanto di un sistema a spinta tangenziale.
Lo
stesso problema visto per la raggiungibilità si pone ora per l'osservabilità.
Di particolare interesse è la possibilità di ottenere un
regolatore a partire da una sola misura di posizione (x1 o x3)
e, quindi, è necessario verificare l'osservabilità
del sistema (A, -, c1’) e del sistema (A, -, c3’).
Dette 01 e 03 le matrici
di osservabilità, si ha
ed
è immediato constatare che O1 non è di rango massimo
(terza riga nulla) mentre O3 lo è. Quindi il sistema
(A, -, c3’) è completamente osservabile ed è così
possibile risalire alle quattro variabili di stato pur di misurare lo scostamento
angolare x3(t) durante un intervallo finito di tempo.
Dall’analisi
fatta di raggiungibilità ed osservabilità, segue che il sistema
(A, b2, c3’) è completamente raggiungibile
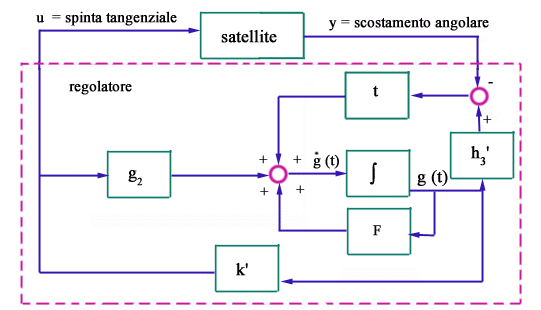
ed osservabile. E’ pertanto possibile determinare un regolatore con lo
schema di figura in modo che gli otto autovalori del sistema ad anello
chiuso così risultante assumano valori prefissati ad arbitrio.
Come appare chiaramente dalla figura, il regolatore è individuato dai quattro parametri l1, l2, l3 e l4 che costituiscono il vettore l dello stimatore e dai quattro parametri k1, k2, k3 e k4 che costituiscono il vettore k della legge di controllo. Il polinomio caratteristico del sistema complessivo è dato dal prodotto dei due polinomi caratteristici delle due matrici (A+b2k’) e (A+lc3’) e, pertanto, per fissare a piacere gli otto autovalori del sistema risultante è sufficiente fissare i quattro autovalori della matrice A+b2k’ (determinando così k’) e, quindi, i quattro autovalori della matrice A+lc3’ (determinando così 1). Ad esempio, detti l1, l2, l3 e l4 i quattro autovalori relativi alla legge di controllo, si ha ma
poiché
si
ottiene
Uguagliando
i coefficienti dei termini di pari grado l
si ottengono così quattro equazioni nelle incognite k1,…,
k4 che certamente ammettono soluzione essendo il sistema completamente
raggiungibile. Allo stesso. modo si procede poi per la matrice A+lc3’
determinando casi 1. quattro parametri dello stimatore asintotico.
|

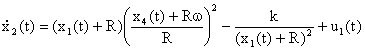 (2.b)
(2.b)

 (3)
(3)