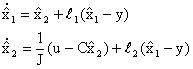|
Come
già visto in precedenti problemi l'antenna con variabile di uscita
uguale alla posizione angolare è un sistema lineare descritto dalle
equazioni
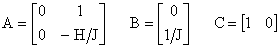
Se
la legge di controllo è di tipo lineare
e
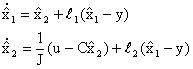
sono determinati per mezzo di uno stimatore asintotico lineareil
polinomio caratteristico
del sistema regolato (che è del quarto ordine) è il prodotto
dei polinomi caratteristici della matrice (A+BK) e della matrice (A+LC)
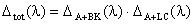
cioèD’altra
parte il polinomio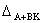
può essere arbitrariamente fissato se e solo se il sistema (A, B,
-) è completamente raggiungibile, mentre il polinomio 
può essere arbitrariamente fissato se e solo se il sistema (A, -,
C) è completamente
osservabile. In conclusione, quindi, i quattro autovalori l1, l2, l3,
e l4
del sistema regolato sono fissabili a valori l1, l2, l3,
e l4
se e solo se l’antenna con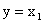 
è un sistema completamente
raggiungibile e osservabile. Poiché le matricisono
entrambe non singolari, si può concludere che nel caso in esame
è possibile sintetizzare un regolatore tale che il sistema risultante
abbia una dinamica arbitrariamente rapida.
I
parametri k1 e k2 che individuano la legge di controllo
e lo stimatore asintotico si possono determinare separatamente con formule
esplicite in cui compaiono le matrici K e O. oppure imponendo (vedi problema
45) che il polinomio caratteristico |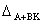
(che dipende dai due parametri k1 e k2) coincida
con il polinomio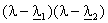 
e che il polinomio 
(che dipende dai due parametri 
) coincida con il polinomio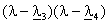 
.
